¶
2.1 Resumen de datos cualitativos
- Distribucion de frecuencia
- Distribuciones de frecuencia relativa y frecuencia potencial
- Gráficas de barras y circulares
2.2 RESUMEN DE DATOS CUANTITATIVOS
- Distribucion de frecuencia
- Distribuciones de frecuencia relativa y frecuencia potencial
- Diagramas de puntos
- Histograma
- Distribuciones acumuladas
- Ojiva
2.3 ANÁLISIS DE DATOS EXPLORATORIOS: EL DIAGRAMA DE TALLO Y HOJA
2.4 TABULACIONES CRUZADAS Y DIAGRAMAS DE DISPERSION
- Tabulacion cruzada
- La paradoja de Simpson
- Diagrama de dispersion y linea de tendencia
2.5 EXTRA
- Glosario
- Formulas clave
- Videos
- Ejercicios propuestos
2.1 RESUME DE DATOS CUALITATIVOS¶
Se introduce el concepto de distribución de frecuencia, que es un resumen tabular de datos que muestra el número de elementos en cada una de varias clases que no se superponen. Se presenta un ejemplo práctico utilizando una muestra de bebidas refrescantes para ilustrar la elaboración e interpretación de una distribución de frecuencia. Se resalta la importancia de comprender cómo se elaboran y cómo deben interpretarse los resúmenes tabulares y gráficos de los datos.
Distribucion de frecuencia¶
La distribución de frecuencia es una manera de organizar datos estadísticos para mostrar la frecuencia con la que ocurren ciertos valores en un conjunto de datos. Básicamente, consiste en agrupar los datos en categorías y contar cuántas veces aparece cada valor en cada una de esas categorías.
Esto se puede presentar en forma de tablas, gráficos de barras, histogramas o gráficos circulares para visualizar la frecuencia de cada valor o rango de valores en tus datos. Es una forma útil de resumir y entender mejor la distribución y patrones dentro de un conjunto de datos.
Distribucion de frecuencia relativa y frecuencia porcentual¶
Una distribución de frecuencia muestra el número de elementos en cada clase que no se superpone, lo que interesa a menudo es la proporción de elementos que pertenecen a cada clase, se determina de la siguiente manera
La frecuencia porcentual es la frecuencia multiplicada por 100. Una distribución de frecuencia relativa da un resumen tabular de los datos que indica la frecuencia de cada clase.
Grafica de barras y circula¶
Es un dispositivo gráfico que se usa para presentar datos cualitativos resumidos en una distribución de frecuencia relativa o porcentual. En un eje se especifican las etiquetas a utilizar y en el otro eje se pone una escala de frecuencia relativa o porcentual, para los datos cualitativos las barras deben estar a una cierta distancia, esto para que cada clase este separada.
EJEMPLO:
import matplotlib.pyplot as plt
# Datos para el gráfico de barras
categorias = ['Capital nacional', 'Capital internacional', 'Renta FIja']
valores = [65, 15, 20]
# Crear la figura y los ejes
fig, ax = plt.subplots()
# Ajustar el color de fondo
ax.set_facecolor("#d4f8b7")
# Pintar el fondo externo del gráfico
fig.patch.set_facecolor('#D4F8B7')
# Crear el gráfico de barras
plt.bar(categorias, valores, color='#5CCB5f', edgecolor='black', linewidth=1.5, width=0.45)
# Añadir etiquetas y título con texto en negrita
plt.xlabel('Tipo de Fondo', fontsize=10, fontweight='bold')
plt.ylabel('Frecuencia Porcentual', fontsize=10, fontweight='bold')
# Mostrar el gráfico
plt.show()
Figura 2.1.1 Ejemplo de Barras Estadistica
La grafica circular o de pastel¶
es otro dispositivo gráfico que presenta para las distribuciones para datos cualitativos. Para realizarla primero se traza un círculo que represente todos los datos, luego se usan las frecuencias relativas para subdividir el círculo en partes que representa la frecuencia relativa de cada clase.
EJEMPLO:
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.gridspec as gridspec
# Datos para el gráfico de pastel
nombres = ['Coke Classic', 'Pepsi', 'Diet Coke', 'Dr. Pepper', 'Sprite']
porcentajes = [38, 26, 16, 10, 10]
colores = ['#5ccb5f', '#98f84a', '#e1ffaf', '#fff', '#e1ffaf']
# Crear el gráfico de pastel sin bordes
fig = plt.figure(figsize=(5, 5))
gs = gridspec.GridSpec(1, 1, width_ratios=[1], height_ratios=[1])
ax = plt.subplot(gs[0])
wedges, texts, autotexts = ax.pie(porcentajes, labels=None, autopct=lambda p: f'{p:.1f}%\n{nombres.pop(0)}', colors=colores)
# Agregar bordes negros a las porciones del gráfico
for wedge in wedges:
wedge.set_edgecolor('black')
wedge.set_linewidth(1)
# Configurar el color de fondo externo
fig.patch.set_facecolor('#D4F8B7')
# Centrar el gráfico en la página
plt.tight_layout()
# Mostrar el gráfico
plt.show()
Figura 2.1.2 Pastel Estadistico
2.2 RESUMEN DE DATOS CUANTITATIVOS¶
Se presentan diferentes métodos para resumir datos cuantitativos, incluyendo la distribución de frecuencia, distribuciones relativas y porcentuales, diagramas de puntos, histogramas, distribuciones acumuladas y ojivas. Se presentan ejemplos prácticos que involucran el análisis de precios de acciones, mostrando la aplicación de estas técnicas en el ámbito económico y empresarial. Se destaca la importancia de comprender y saber interpretar los métodos tabulares y gráficos para resumir datos.
Distribucion de frecuencia¶
Esta distribución expresa la frecuencia de cada valor o categoría como una proporción del total de observaciones en el conjunto de datos. Se calcula dividiendo la frecuencia de cada valor entre el número total de observaciones.
La distribución de frecuencia es una forma de organizar y resumir datos cuantitativos. Consiste en contar y clasificar la frecuencia con la que ocurren diferentes valores en un conjunto de datos. El objetivo es proporcionar una visión clara y concisa de cómo se distribuyen los valores en el conjunto de datos.
Distribucion de frecuencia relativa y frecuencia porcentual¶
La distribución de frecuencia relativa y la frecuencia porcentual son dos formas de expresar la frecuencia de ocurrencia de valores en un conjunto de datos en relación con el total de datos.
La distribución de frecuencia relativa y la frecuencia porcentual son formas de expresar la frecuencia de los datos en relación con el total del conjunto de datos. Estas medidas son útiles para entender la proporción de cada categoría o intervalo con respecto al conjunto completo.
Ancho de clase:¶
Como regla general el ancho debe ser igual para todas las clases, por lo que el número y ancho de la clase no son decisiones independientes, se utiliza la siguiente expresión para determinar el ancho de la clase:
Histograma¶
Un histograma es una representación gráfica de la distribución de un conjunto de datos. Se utiliza comúnmente en estadísticas para visualizar la frecuencia de ocurrencia de distintos valores en un conjunto de datos continuo. Aquí hay una descripción básica de cómo se construye un histograma:
-Definición de clases: Divide el rango total de datos en intervalos o "clases". Cada clase representa un rango específico de valores. Los límites de clase (inferior y superior) se definen para cada intervalo.
-Conteo de frecuencias: Determina cuántas observaciones caen dentro de cada clase. Este conteo se conoce como la frecuencia de la clase.
-Construcción del gráfico: Dibuja un rectángulo para cada clase, cuya base es el intervalo de clase y la altura es proporcional a la frecuencia de esa clase. Puedes utilizar barras contiguas o separadas, dependiendo de tus preferencias o estándares.
-Ejes del histograma: Etiqueta los ejes. El eje horizontal representa la variable que estás midiendo (por ejemplo, valores), y el eje vertical representa la frecuencia o densidad de frecuencia.
Límite de clase¶
Es un concepto utilizado en estadística, especialmente en la construcción de histogramas y en la organización de datos en intervalos. Cada conjunto de datos se divide en intervalos o clases, y el límite de clase se refiere a los valores que definen el inicio y el final de cada intervalo.
Hay dos tipos principales de límites de clase:
-Límite inferior de clase: Es el valor más pequeño que puede pertenecer a una clase. Es el límite que separa una clase de la siguiente.
-Límite superior de clase: Es el valor más grande que puede pertenecer a una clase. Es el límite que separa una clase de la siguiente.
Por ejemplo, si tienes datos agrupados en clases de 10 a 19, el límite inferior de la clase es 10 y el límite superior es 19. El límite de clase ayuda a definir claramente los intervalos en los cuales se agrupan los datos.
La longitud de clase se calcula restando el límite inferior del límite superior. Esto es importante al construir histogramas para asegurar que las barras se ajusten correctamente a los datos y proporcionen una representación precisa de la distribución.
Diagrama de puntos¶
Un diagrama de puntos es una representación gráfica de datos unidimensionales en la que cada observación se representa mediante un punto en una línea. Este tipo de gráfico es especialmente útil para visualizar la distribución y concentración de los valores en un conjunto de datos. El eje horizontal representa la variable de interés, mientras que el eje vertical muestra la frecuencia o la cantidad de veces que ocurre cada valor. Los puntos se colocan en la línea de acuerdo con el valor de la observación, permitiendo identificar patrones, tendencias o la dispersión de los datos.
Distribuciones acumuladas¶
Son útiles para analizar la posición relativa de un valor en un conjunto de datos, entender la cantidad o proporción de datos por debajo de cierto umbral y comparar la distribución de diferentes conjuntos de datos.
Estos datos se pueden representar visualmente mediante gráficos acumulados, como los gráficos de frecuencia acumulada o los diagramas de polígono de frecuencia acumulada, que muestran la acumulación de frecuencias a lo largo de los valores de los datos.
Ojiva¶
La gráfica de una distribución, llamada ojiva, muestra los valores de los datos sobre eje horizontal y las frecuencias en el eje vertical.Es un tipo específico de gráfico utilizado en estadísticas para representar la distribución acumulada de frecuencias o porcentajes de un conjunto de datos. También se conoce como gráfico de frecuencia acumulada.
Una ojiva se construye trazando puntos o marcando los extremos superiores de las barras de un histograma, y luego uniendo estos puntos sucesivamente con líneas suaves para formar una curva. Esta curva representa la acumulación gradual de frecuencias o porcentajes a lo largo de los valores de los datos.
La ojiva es útil para visualizar cómo se acumulan los datos a lo largo de un rango de valores y proporciona una comprensión intuitiva de la distribución de los datos en términos de su posición relativa. Puede ser particularmente útil para identificar tendencias o patrones generales en la distribución de los datos.
Además, la ojiva permite comparar fácilmente varias distribuciones acumuladas y observar diferencias o similitudes entre conjuntos de datos diferentes. Esta representación gráfica es comúnmente utilizada en análisis estadístico para comprender la distribución acumulada de frecuencias o porcentajes en conjuntos de datos numéricos.
Ejercicios¶
Ejemplo 1.
En una tienda de autos, se registra la cantidad de autos Toyota vendidos en cada día del mes de Setiembre.
0; 1; 2; 1; 2; 0; 3; 2; 4; 0; 4; 2; 1; 0; 3; 0; 0; 3; 4; 2; 0; 1; 1; 3; 0; 1; 2; 1; 2; 3
Con los datos obtenidos, elaborar una tabla de frecuencias.
Solución:
En la primera columna, colocamos los valores de nuestra variable, en la segunda la frecuencia absoluta, luego la frecuencia acumulada, seguida por la frecuencia relativa, y finalmente la frecuencia relativa acumulada. Ahora vamos a agregar la columna de frecuencia porcentual, y frecuencia porcentual acumulada.
Tabla 2.2.1
| Autos vendidos | Frecuencia absoluta | Frecuencia acumulada | Frecuencia relativa | Frec. relativa acumulada | Frecuencia porcentual | Frec. porcentual acumulada |
|---|---|---|---|---|---|---|
| 0 | 8 | 8 | 0,267 | 0,267 | 26,7% | 26,7% |
| 1 | 7 | 15 | 0,233 | 0,500 | 23,3% | 50,0% |
| 2 | 7 | 22 | 0,233 | 0,733 | 23,3% | 73,3% |
| 3 | 5 | 27 | 0,167 | 0,900 | 16,7% | 90,0% |
| 4 | 3 | 30 | 0,100 | 1 | 10,0% | 100% |
| Total | 30 | 1 | 100% |
Grafica:
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.gridspec as gridspec
# Datos para el gráfico de pastel
nombres = ['0 autos vendidos', '1 autos vendidos', '2 autos vendidos', '3 autos vendidos', '4 autos vendidos']
porcentajes = [26.7,23.3,23.3,16.7,10.0]
colores = ['#5ccb5f', '#98f84a', '#e1ffaf', '#fff', '#e1ffaf']
# Crear el gráfico de pastel sin bordes
fig = plt.figure(figsize=(5, 5))
gs = gridspec.GridSpec(1, 1, width_ratios=[1], height_ratios=[1])
ax = plt.subplot(gs[0])
wedges, texts, autotexts = ax.pie(porcentajes, labels=None, autopct=lambda p: f'{p:.1f}%\n{nombres.pop(0)}', colors=colores)
# Agregar bordes negros a las porciones del gráfico
for wedge in wedges:
wedge.set_edgecolor('black')
wedge.set_linewidth(1)
# Configurar el color de fondo externo
fig.patch.set_facecolor('#D4F8B7')
# Centrar el gráfico en la página
plt.tight_layout()
# Mostrar el gráfico
plt.show()
Ejemplo 2
Se le pidió a un grupo de personas que indiquen su color favorito, y se obtuvo los siguientes resultados:
Tabla 2.2.2
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | Negro | Azul | Amarillo | Rojo | Azul |
| 2 | Azul | Rojo | Negro | Amarillo | Rojo |
| 3 | Rojo | Amarillo | Amarillo | Azul | Rojo |
| 4 | Negro | Azul | Rojo | Negro | Amarillo |
Con los resultados obtenidos, elaborar una tabla de frecuencias.
Solución:
En la primera columna, colocamos los valores de nuestra variable, en la segunda la frecuencia absoluta, luego la frecuencia acumulada, seguida por la frecuencia relativa, y finalmente la frecuencia relativa acumulada. Por ser el primer problema, no haremos uso de las frecuencias porcentuales.
Tabla 2.2.3
| Color | Frecuencia absoluta | Frecuencia acumulada | Frecuencia relativa | Frec. relativa acumulada |
|---|---|---|---|---|
| Negro | 4 | 4 | 0,20 | 0,20 |
| Azul | 5 | 9 | 0,25 | 0,45 |
| Amarillo | 5 | 14 | 0,25 | 0,70 |
| Rojo | 6 | 20 | 0,30 | 1 |
| Total | 20 | 1 |
Grafica:
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.gridspec as gridspec
# Datos para el gráfico de pastel
nombres = ['Negro', 'Azul', 'Amarillo', 'Rojo']
porcentajes = [20,25,25,30]
colores = ['#5ccb5f', '#98f84a', '#e1ffaf', '#fff', '#e1ffaf']
# Crear el gráfico de pastel sin bordes
fig = plt.figure(figsize=(5, 5))
gs = gridspec.GridSpec(1, 1, width_ratios=[1], height_ratios=[1])
ax = plt.subplot(gs[0])
wedges, texts, autotexts = ax.pie(porcentajes, labels=None, autopct=lambda p: f'{p:.1f}%\n{nombres.pop(0)}', colors=colores)
# Agregar bordes negros a las porciones del gráfico
for wedge in wedges:
wedge.set_edgecolor('black')
wedge.set_linewidth(1)
# Configurar el color de fondo externo
fig.patch.set_facecolor('#D4F8B7')
# Centrar el gráfico en la página
plt.tight_layout()
# Mostrar el gráfico
plt.show()
Ejercicio 3.
Las notas de 35 alumnos en el examen final de estadística, calificado del 0 al 10, son las siguientes:
0; 0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 7; 7; 7; 8; 8; 8; 9; 10; 10.
Con los datos obtenidos, elaborar una tabla de frecuencias con 5 intervalos o clases. Solución:
• Hallamos el rango: R = Xmax– Xmin = 10 – 0 = 10.
• El número de intervalos (k), me lo da el enunciado del problema: k = 5.
• Calculamos la amplitud de clase: A = R/k = 10/5 = 2.
• Ahora hallamos los límites inferiores y superiores de cada clase, y elaboramos la tabla de frecuencias.
Tabla 2.2.4
| Intervalo | Marca de clase | Frecuencia absoluta | Frecuencia acumulada | Frecuencia relativa | Frec. relativa acumulada |
|---|---|---|---|---|---|
| [0 – 2) | 1 | 8 | 8 | 0,229 | 0,229 |
| [2 – 4) | 3 | 7 | 15 | 0,200 | 0,429 |
| [4 – 6) | 5 | 8 | 23 | 0,229 | 0,658 |
| [6 – 8) | 7 | 6 | 29 | 0,171 | 0,829 |
| [8 – 10] | 9 | 6 | 35 | 0,171 | 1 |
| Total | - | 35 | - | 1 | - |
Grafica:
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.gridspec as gridspec
# Datos para el gráfico de pastel
nombres = ['[0-2)','[2-4)','[4-6)','[6-8)','[8-10]']
porcentajes = [22.9,20.0,22.9,17.1,17.1]
colores = ['#5ccb5f', '#98f84a', '#e1ffaf', '#fff', '#e1ffaf']
# Crear el gráfico de pastel sin bordes
fig = plt.figure(figsize=(5, 5))
gs = gridspec.GridSpec(1, 1, width_ratios=[1], height_ratios=[1])
ax = plt.subplot(gs[0])
wedges, texts, autotexts = ax.pie(porcentajes, labels=None, autopct=lambda p: f'{p:.1f}%\n{nombres.pop(0)}', colors=colores)
# Agregar bordes negros a las porciones del gráfico
for wedge in wedges:
wedge.set_edgecolor('black')
wedge.set_linewidth(1)
# Configurar el color de fondo externo
fig.patch.set_facecolor('#D4F8B7')
# Centrar el gráfico en la página
plt.tight_layout()
# Mostrar el gráfico
plt.show()
Ejercicio 4.
Un grupo de atletas se está preparando para una maratón siguiendo una dieta muy estricta. A continuación, viene el peso en kilogramos que ha logrado bajar cada atleta gracias a la dieta y ejercicios.
Tabla 2.2.5
| 0,2 | 8,4 | 14,3 | 6,5 | 3,4 |
| 4,6 | 9,1 | 4,3 | 3,5 | 1,5 |
| 6,4 | 15,2 | 16,1 | 19,8 | 5,4 |
| 12,1 | 9,6 | 8,7 | 12,1 | 3,2 |
Hallar la amplitud de clase.
Solución:
• Hallamos el rango: R = Xmax– Xmin = 19,8 – 0,2 = 19,6.
• El número de intervalos (k), lo calculamos usando la regla de Sturges: k = 1 + 3,322log(n) = 1 + 3,322.log(20) = 5,32. Podemos redondear el valor de k a 5
• Calculamos la amplitud de clase: A = R/k = 19,6/5 = 3,92. Redondeamos a 4.
Ejercicio 5.
Representa en un diagrama de puntos los siguientes datos obtenidos de las notas de un examen:
Tabla de Notas de Examen por Estudiante
| Estudiantes | Nota Examen |
|---|---|
| Estudiante 1 | 7 |
| Estudiante 2 | 6 |
| Estudiante 3 | 5 |
| Estudiante 4 | 4 |
| Estudiante 5 | 8 |
| Estudiante 6 | 10 |
| Estudiante 7 | 3 |
| Estudiante 8 | 5 |
| Estudiante 9 | 1 |
| Estudiante 10 | 6 |
| Estudiante 11 | 7 |
| Estudiante 12 | 4 |
| Estudiante 13 | 5 |
| Estudiante 14 | 5 |
| Estudiante 15 | 7 |
| Estudiante 16 | 6 |
| Estudiante 17 | 5 |
| Estudiante 18 | 8 |
| Estudiante 19 | 9 |
| Estudiante 20 | 7 |
En primer lugar, tenemos que dibujar una recta numérica para poder representar los datos. Así que trazamos una línea horizontal y en ella representamos todos los valores que aparecen en la muestra.

Y ahora dibujamos un punto encima de cada número por cada vez que aparece en la tabla de datos. Por ejemplo, el número 4 está repetido dos veces, por lo tanto, representaremos dos puntos en la recta numérica encima del número 4.

De esta forma ya hemos elaborado el gráfico de puntos. Pero aún nos queda interpretar el diagrama de puntos obtenido.
Para analizar el diagrama de puntos, debemos fijarnos en la distribución de los datos, es decir, debemos fijarnos en la dispersión del diagrama de puntos. En este caso, las notas que más se repiten están en el centro del diagrama, por lo que la mayoría de alumnos han sacado notas entre el 5 y el 7. De hecho, la moda del diagrama de puntos es el número cinco.
Por otro lado, ningún alumno ha sacado un dos, ya que no aparece ni una sola vez en la tabla de valores. Por eso no tiene representado ningún punto encima.
Finalmente, cabe destacar que los datos de este ejemplo se tratan de números enteros, pero también se puede hacer un diagrama de puntos con números decimales. Incluso se puede hacer un diagrama de puntos con datos cualitativos.
Ejercicio 6.
Se desea saber cuántos libros se leyeron 10 estudiantes en el verano.
Tabla de Estudiantes y Libros
| Estudiantes | Libros |
|---|---|
| Estudiante 1 | 5 |
| Estudiante 2 | 1 |
| Estudiante 3 | 2 |
| Estudiante 4 | 5 |
| Estudiante 5 | 8 |
| Estudiante 6 | 0 |
| Estudiante 7 | 3 |
| Estudiante 8 | 2 |
| Estudiante 9 | 2 |
| Estudiante 10 | 1 |
• Lo primero es organizar los datos de menor a mayor, sin importar que se repitan.
0; 1; 1; 2; 2; 2; 3; 5; 5; 8.
• Segundo trazamos una recta numérica con los números del cero (número menor) hasta el ocho (número mayor).
• Tercero en la recta numérica colocamos un punto en cada uno de los números que aparecen el primer paso, colocando en el cero un punto, en el uno dos puntos, en los dos tres puntos, en el tres un punto, el número cuatro no se le ponen puntos y así sucesivamente.
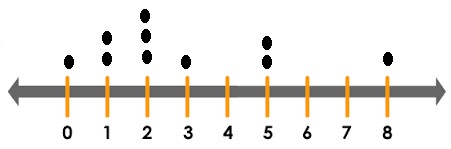
Observa el siguiente video para que te quede un poco más claro cómo construir los diagramas de puntos:
from IPython.display import YouTubeVideo
youtube_video = YouTubeVideo('bAY5zmtgjDI')
display(youtube_video)
2.3 ÁNALISIS DE DATOS EXPLORATORIOS: EL DIAGRAMA DE TALLO Y HOJA¶
Se presenta el concepto de diagrama de tallo y hoja como una herramienta para resumir datos cuantitativos y se explica cómo construir uno. Se presentan ejemplos prácticos que involucran el análisis de datos de duración de auditorías y se destaca la importancia de comprender y saber interpretar los diagramas de tallo y hoja para resumir datos. Además, se mencionan otras herramientas de análisis exploratorio, como la tabla de frecuencia y el diagrama de caja y bigotes.
Estas técnicas consisten en una aritmética simple y gráficas fáciles de elaborar para resumir los datos rápidamente, una de ellas es el tallo y hoja, donde muestra simultáneamente la clasificación y la forma de un conjunto de datos. Tiene dos ventajas
- Es fácil de elaborar a mano.
- Proporciona más información que el histograma
Ejercicios¶
Ejercicio 1.
En la clase de Precálculo de primavera de Susan Dean las calificaciones del primer examen fueron las siguientes (de menor a mayor):
33; 42; 49; 49; 53; 55; 55; 61; 63; 67; 68; 68; 69; 69; 72; 73; 74; 78; 80; 83; 88; 88; 88; 90; 92; 94; 94; 94; 94; 96; 100
Tabla 2.3.1
| Tallo | Hoja |
|---|---|
| 3 | 3 |
| 4 | 2 9 9 |
| 5 | 3 5 5 |
| 6 | 1 3 7 8 8 9 9 |
| 7 | 2 3 4 8 |
| 8 | 0 3 8 8 8 |
| 9 | 0 2 4 4 4 4 6 |
| 10 | 0 |
El gráfico de tallo muestra que la mayoría de las calificaciones fueron de 60, 70, 80 y 90. Ocho de las 31 calificaciones, es decir, aproximadamente el 26 % (8/31) estaban en los 90 o 100, un número bastante alto de calificaciones con A.
Ejercicio 2.
El diagrama de tallo y hoja bilateral permite comparar los dos conjuntos de datos en dos columnas. En el diagrama de tallo y hoja bilateral dos conjuntos de hojas comparten el mismo tallo. Las hojas están a la izquierda y a la derecha de los tallos. La Tabla 1 y la Tabla 2 muestran las edades de los presidentes en su investidura y al momento de su muerte. Construya un diagrama de tallo y hoja bilateral utilizando estos datos.
Tabla 2.3.2 Edades de los presidentes en su investidura
| Presidente | Edad | Presidente | Edad | Presidente | Edad |
|---|---|---|---|---|---|
| Washington | 57 | Lincoln | 52 | Hoover | 54 |
| J. Adams | 61 | A. Johnson | 56 | F. Roosevelt | 51 |
| Jefferson | 57 | Grant | 46 | Truman | 60 |
| Madison | 57 | Hayes | 54 | Eisenhower | 62 |
| Monroe | 58 | Garfield | 49 | Kennedy | 43 |
| J. Q. Adams | 57 | Arthur | 51 | L. Johnson | 55 |
| Jackson | 61 | Cleveland | 47 | Nixon | 56 |
| Van Buren | 54 | B. Harrison | 55 | Ford | 61 |
| W. H. Harrison | 68 | Cleveland | 55 | Carter | 52 |
| Tyler | 51 | McKinley | 54 | Reagan | 69 |
| Polk | 49 | T. Roosevelt | 42 | G. H. W. Bush | 64 |
| Taylor | 64 | Taft | 51 | Clinton | 47 |
| Fillmore | 50 | Wilson | 56 | G. W. Bush | 54 |
| Pierce | 48 | Harding | 55 | Obama | 47 |
| Buchanan | 65 | Coolidge | 51 |
Tabla 2.3.3 Titulo de la Tabla
| Presidente | Edad | Presidente | Edad | Presidente | Edad |
|---|---|---|---|---|---|
| Washington | 67 | Lincoln | 56 | Hoover | 90 |
| J. Adams | 90 | A. Johnson | 66 | F. Roosevelt | 63 |
| Jefferson | 83 | Grant | 63 | Truman | 88 |
| Madison | 85 | Hayes | 70 | Eisenhower | 78 |
| Monroe | 73 | Garfield | 49 | Kennedy | 46 |
| J. Q. Adams | 80 | Arthur | 56 | L. Johnson | 64 |
| Jackson | 78 | Cleveland | 71 | Nixon | 81 |
| Van Buren | 79 | B. Harrison | 67 | Ford | 93 |
| W. H. Harrison | 68 | Cleveland | 71 | Reagan | 93 |
| Tyler | 71 | McKinley | 58 | ||
| Polk | 53 | T. Roosevelt | 60 | ||
| Taylor | 65 | Taft | 72 | ||
| Fillmore | 74 | Wilson | 67 | ||
| Pierce | 64 | Harding | 57 | ||
| Buchanan | 77 | Coolidge | 60 |
Tabla 2.3.4 Solucion
| Edades en la investidura | Edades al momento de la muerte | |
|---|---|---|
| 9 9 8 7 7 7 6 3 2 | 4 | 6 9 |
| 8 7 7 7 7 6 6 6 5 5 5 5 4 4 4 4 4 2 2 1 1 1 1 1 0 | 5 | 3 6 6 7 7 8 |
| 6 | 0 0 3 3 4 4 5 6 7 7 7 8 | |
| 7 | 0 0 1 1 1 4 7 8 8 9 | |
| 8 | 0 1 3 5 8 | |
| 9 | 0 0 3 3 |
Ejercicio 3.
En las pruebas médicas de un instituto, se toma la altura de los cuarenta alumnos de una clase. El médico está interesado en representar gráficamente la variable y opta por el diagrama de tallo y hoja.
Ordena las alturas en una tabla:
Tabla 2.3.5
| Altura de los Alumnos |
|---|
| 145 |
| 147 |
| 149 |
| 152 |
| 153 |
| 154 |
| 154 |
| 156 |
| 157 |
| 158 |
| 162 |
| 162 |
| 162 |
| 163 |
| 163 |
| 164 |
| 164 |
| 165 |
| 167 |
| 167 |
| 168 |
| 169 |
| 169 |
| 170 |
| 171 |
| 171 |
| 172 |
| 173 |
| 174 |
| 174 |
| 175 |
| 176 |
| 176 |
| 179 |
| 180 |
| 181 |
| 183 |
| 185 |
| 185 |
| 186 |
Los datos son tomados en centímetros, por lo que tiene tres cifras cada número. En este caso no se requiere redondear los datos, ya que se parte del número de dígitos que se desea. Los dos primeros dígitos serán el tallo y el último la hoja.
Una vez preparados los datos, procede a construir el diagrama. Dibuja una tabla con dos columnas. En la primera columna coloca los tallos ordenados de menor a mayor. En este caso los tallos serán: 14, 15, 16, 17 y 18.
Se registra en la segunda columna todas las hojas, debidamente ordenadas, junto al tallo correspondiente:
Tabla 2.3.6
| Tallo | Hoja |
|---|---|
| 14 | 5 7 9 |
| 15 | 2 3 4 4 6 7 8 |
| 16 | 2 2 2 3 3 4 4 5 7 7 8 9 9 |
| 17 | 0 1 1 2 3 4 4 5 6 6 8 9 |
| 18 | 0 1 3 5 6 |
2.4 TABULACIONES CRUZADAS Y DIAGRAMAS DE DISPERSIÓN¶
Se mencionan diferentes herramientas para resumir datos cualitativos y cuantitativos, como la distribución de frecuencia, distribuciones relativas y porcentuales, diagramas de puntos, histogramas, distribuciones acumuladas, ojivas, tabulaciones cruzadas y diagramas de dispersión. Se destaca la importancia de comprender y saber interpretar estos métodos para el análisis estadístico en el ámbito empresarial y económico. Además, se menciona que con conjuntos de datos grandes, el software de computadora es fundamental para la elaboración de resúmenes tabulares y gráficos de los datos.
Tabulacion cruzada¶
La tabulación cruzada, también conocida como tabla de contingencia, es una herramienta estadística que se utiliza para resumir y analizar la relación entre dos variables categóricas. En una tabla de contingencia, los datos se organizan en filas y columnas, donde cada celda muestra la frecuencia o conteo de casos que caen en una categoría específica de ambas variables.
A continuación, te proporciono un ejemplo sencillo y cómo se vería en una tabla de contingencia:
Supongamos que tienes dos variables categóricas: Género (Masculino/Femenino) y Preferencia de Deporte (Fútbol/Baloncesto). Has recopilado datos sobre 100 personas.
Tabla 2.3.4 Solucion
| Fútbol | Baloncesto | |
|---|---|---|
| Masculino | 20 | 30 |
| Femenino | 15 | 35 |
En esta tabla, cada celda representa el número de personas que cumplen con una combinación específica de género y preferencia de deporte. Por ejemplo, hay 20 personas masculinas que prefieren el fútbol, y 35 personas femeninas que prefieren el baloncesto.
La tabulación cruzada es útil para explorar y entender las relaciones entre dos variables categóricas. Además, puede ser la base para realizar pruebas estadísticas como la prueba de independencia chi-cuadrado, que evalúa si hay una asociación significativa entre las dos variables.
En términos de software, puedes utilizar herramientas estadísticas como R, Python con pandas, o incluso software de hojas de cálculo como Excel para realizar tabulaciones cruzadas.
La paradoja de Simpson¶
La paradoja de Simpson es un fenómeno estadístico en el que una tendencia que aparece en diferentes grupos de datos desaparece o se invierte cuando se combinan estos grupos. Específicamente, la paradoja ocurre cuando una relación que es presente en subgrupos de datos se revierte cuando se agregan esos subgrupos.
Esta paradoja puede surgir cuando las diferencias en los tamaños de los subgrupos no se tienen en cuenta adecuadamente al interpretar los resultados. Puede conducir a conclusiones erróneas si no se considera cuidadosamente la estructura de los datos.
Un ejemplo clásico de la paradoja de Simpson se encuentra en el contexto de tasas de éxito en dos tratamientos diferentes. Puede suceder que, al observar cada subgrupo por separado, un tratamiento parezca ser más efectivo. Sin embargo, al combinar los grupos, el resultado general puede mostrar que el otro tratamiento es más efectivo. Esto puede ocurrir si los subgrupos tienen tamaños diferentes y las tasas de éxito y fallo varían significativamente entre ellos.
La paradoja de Simpson destaca la importancia de considerar el tamaño de las muestras y las variables relevantes al interpretar datos y resultados estadísticos. Es un recordatorio de que las conclusiones basadas en agregados pueden no reflejar necesariamente las tendencias en subgrupos más pequeños y resalta la necesidad de un análisis más detallado y contextualizado.
Diagrama de dispersión y línea de tendencia¶
Un diagrama de dispersión es una herramienta gráfica que representa la relación entre dos variables. Cada punto en el gráfico corresponde a un par de valores de las dos variables. Este tipo de gráfico es útil para visualizar patrones, tendencias y la fuerza de la relación entre las variables.
Aquí está la descripción general de cómo crear un diagrama de dispersión:
-Ejes: Coloca una variable en el eje horizontal (eje x) y la otra en el eje vertical (eje y).
-Puntos: Para cada observación en tu conjunto de datos, coloca un punto en el gráfico con coordenadas (x, y) según los valores de las dos variables.
-Patrones y Tendencias: Examina la distribución de los puntos para identificar patrones o tendencias. Si los puntos se agrupan en una dirección particular, puede indicar una relación entre las variables.
La línea de tendencia es una línea que intenta modelar la relación general entre las dos variables. Puede ser una recta (regresión lineal) o una curva (regresión no lineal). La línea de tendencia proporciona una representación visual de la dirección y la fuerza de la relación.
Ejercicios¶
Ejercicio 1.
En el ejemplo se supone que, en un día de lluvia, un estudiante cuenta cuántas personas "con" y cuántas "sin" paraguas acuden a la clase de estadística. Además, el alumno anota el sexo de los estudiantes.
Tabla de Paraguas por Sexo
| Sexo | Con Paraguas |
|---|---|
| mujer | Sí |
| hombre | Sí |
| mujer | Sí |
| mujer | Sí |
| hombre | Sí |
| hombre | No |
| mujer | No |
| hombre | No |
| mujer | No |
| mujer | No |
| hombre | No |
| mujer | Sí |
| hombre | Sí |
| mujer | Sí |
| hombre | Sí |
| hombre | No |
| mujer | No |
| hombre | No |
| mujer | No |
| mujer | No |
| mujer | No |
El resultado puede mostrarse ahora fácilmente en una tabla de contingencia. La tabla de clasificación cruzada contiene ahora las frecuencias absolutas de las respectivas combinaciones de características. Esto se calcula como sigue:
Tabla de Paraguas por Sexo
| Con Paraguas | sin Paraguas | Total | |
|---|---|---|---|
| mujer | 5 | 7 | 12 |
| hombre | 5 | 5 | 10 |
| Total | 10 | 12 | 22 |
Por ejemplo, una investigación sobre la intención de voto arroja los siguientes resultados:
Género de la población investigada: Masculino 45% Femenino 55%
¿Asistirá a votar? Si 70% No 30%
Ante estos resultados, surge la interrogante: ¿Qué porcentaje de hombres y de mujeres votarán? O ¿Qué porcentaje de hombre y mujeres se abstendrán de votar?
La tabulación cruzada nos puede ayudar a resolver estas interrogantes, y una nueva tabla podría quedar conformada de la siguiente manera, tomando de base los resultados obtenidos:
Tabla de Votos por Género
| Género / Voto | Si | No | Total |
|---|---|---|---|
| Femenino | 33% | 22% | 55% |
| Masculino | 37% | 8% | 45% |
| Total | 70% | 30% | 100% |
Y a partir de la tabla anterior, ya se pueden realizar análisis más profundos y llegar a conclusiones de mayor peso que solamente con la información que teníamos en un principio. Esto gracias a la Tabulación Cruzada. Ocurre entonces, que en ocasiones tenemos una base de datos enorme, pero que no logramos encontrar la forma de obtener más información a partir de la misma, y es aquí en donde el SPSS nos puede colaborar construyendo tabulaciones cruzadas con todas las variables que deseemos, y con un uso óptimo del tiempo.
Ejercicio 2.
En la tabla siguiente se muestran los géneros y el uso de las manos de una muestra poblacional de 12 individuos:
Tabla de Uso de las Manos por Género
| Muestra # | Género | Uso de las manos |
|---|---|---|
| 1 | Mujer | Diestra/o |
| 2 | Varón | Zurda/o |
| 3 | Varón | Diestra/o |
| 4 | Mujer | Diestra/o |
| 5 | Mujer | Diestra/o |
| 6 | Varón | Diestra/o |
| 7 | Varón | Zurda/o |
| 8 | Varón | Diestra/o |
| 9 | Mujer | Diestra/o |
| 10 | Mujer | Zurda/o |
| 11 | Varón | Diestra/o |
| 12 | Mujer | Diestra/o |
La tabulación cruzada conduce hacia la siguiente tabla de contingencia:
Tabla de Uso de Manos por Género
| Diestra/o | Zurda/o | Total | |
|---|---|---|---|
| Mujeres | 5 | 1 | 6 |
| Varones | 4 | 2 | 6 |
| Total | 9 | 3 | 12 |
La paradoja de Simpson
Supongamos que se quiere realizar un estudio comparado de la efectividad de una cierta cirugía en dos hospitales A y B, para lo cual se obtienen los datos presentados en la Tabla 1. Se pide analizar los datos y determinar cuál hospital da mayor tasa de supervivencia
Tabla de Comparación de Supervivencia a Cirugía
| Hospital A | Hospital B | |
|---|---|---|
| Mueren | 63 | 16 |
| Sobreviven | 2037 | 784 |
| Total pacientes operados | 2100 | 800 |
Si analizamos los datos de la Tabla 1, se puede observar que en el hospital A, muere el 3% (63/2100) de los pacientes que se somete a la cirugía y en el hospital B el 2% (16/800), por lo que inicialmente estos resultados nos podrían llevar a pensar que el hospital más seguro para someterse a dicha operación sería el hospital B. La paradoja aparece cuando controlamos los resultados teniendo en cuenta otras variables que influyen en la supervivencia, por ejemplo, el “estado de salud de los pacientes antes de la operación”.
2.5 Extra¶
Glosario¶
- Frecuencia porcentual: fórmula para calcular la frecuencia porcentual de una clase en una distribución de frecuencia. Se calcula multiplicando la frecuencia relativa por 100.
- Frecuencia acumulada: fórmula para calcular la frecuencia acumulada de una clase en una distribución de frecuencia. Se calcula sumando las frecuencias de todas las clases anteriores, incluyendo la propia.
- Frecuencia relativa acumulada: fórmula para calcular la frecuencia relativa acumulada de una clase en una distribución de frecuencia. Se calcula dividiendo la frecuencia acumulada de la clase entre el tamaño total de la muestra.
- Tabulación cruzada: fórmula para construir una tabla de frecuencia cruzada, que muestra la frecuencia conjunta de dos variables.
- Coeficiente de correlación: fórmula para calcular el coeficiente de correlación entre dos variables en un diagrama de dispersión. Se calcula dividiendo la covarianza entre las desviaciones estándar de las dos variables.
- Recta de regresión: fórmula para calcular la recta de regresión en un diagrama de dispersión. Se calcula utilizando la media y la desviación estándar de las dos variables y el coeficiente de correlación.
Fórmulas Clave¶
-Uso del MiniTab para presentaciones tabulares y gráficas.- El uso de Minitab para presentaciones tabulares y gráficas es fundamental en el análisis estadístico. Minitab ofrece amplias capacidades para elaborar resúmenes tabulares y gráficos de los datos. Permite la elaboración de varios resúmenes gráficos y tabulares, incluyendo el diagrama de puntos, el histograma, el diagrama de tallo y hoja, el diagrama de dispersión y la tabulación cruzada. Además, Minitab proporciona opciones para personalizar los gráficos, como ajustar el eje x para que los valores numéricos aparezcan en los puntos medios de los rectángulos del histograma. Estas capacidades son esenciales para el análisis detallado de los datos y la presentación visual de los resultados.
-Uso del Excel para presentaciones tabulares y graficas.- El uso de Excel para presentaciones tabulares y gráficas es una herramienta común en el análisis de datos. Excel ofrece la capacidad de crear una variedad de gráficos, incluyendo gráficos de barras, gráficos circulares, diagramas de dispersión, entre otros. Además, Excel permite la creación de tablas dinámicas para resumir y analizar grandes conjuntos de datos de manera eficiente. Estas funciones son útiles para la presentación visual de los datos y el análisis detallado de la información. Además, Excel proporciona opciones para personalizar los gráficos, como ajustar los ejes y seleccionar diferentes estilos de gráficos. Estas capacidades hacen de Excel una herramienta versátil para la presentación y análisis de datos
Videos¶
Espacio para videos que reforzaran nuestro conocimiento y aclarar dudas:
Diferencias entre Cuantitativa y Cualitativa:
from IPython.display import YouTubeVideo
youtube_video = YouTubeVideo('uWxmy1vOS88')
display(youtube_video)
from IPython.display import YouTubeVideo
youtube_video = YouTubeVideo('nCszHELuwxk')
display(youtube_video)
Histogramas de frecuencia:
from IPython.display import YouTubeVideo
youtube_video = YouTubeVideo('-VZ4x_rLCHE')
display(youtube_video)
Ojivas:
from IPython.display import YouTubeVideo
youtube_video = YouTubeVideo('p90bzl1cdDM')
display(youtube_video)
Diagrama de tallos y hojas:
from IPython.display import YouTubeVideo
youtube_video = YouTubeVideo('DZWxasd0Exk')
display(youtube_video)
Diagrama de dispercion:**
from IPython.display import YouTubeVideo
youtube_video = YouTubeVideo('hTIXDHrGs5A')
display(youtube_video)
Tabulacion cruzada:
from IPython.display import YouTubeVideo
youtube_video = YouTubeVideo('-x6UYTVyCns')
display(youtube_video)
Ejercicios¶
Ejercicio 1.
Nielsen Home Technology Report informa sobre la tecnología en el hogar y su uso. Los datos siguientes son las horas de uso de computadora por semana en una muestra de 50 personas.
Tabla de Números Decimales
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.1 | 1.5 | 10.4 | 5.9 | 3.4 | 5.7 | 1.6 | 6.1 | 3.0 | 3.7 | 3.1 | 4.8 |
| 2.0 | 14.8 | 5.4 | 4.2 | 3.9 | 4.1 | 11.1 | 3.5 | 4.1 | 4.1 | 8.8 | 5.6 |
| 4.3 | 3.3 | 7.1 | 10.3 | 6.2 | 7.6 | 10.8 | 2.8 | 9.5 | 12.9 | 12.1 | 0.7 |
| 4.0 | 9.2 | 4.4 | 5.7 | 7.2 | 6.1 | 5.7 | 5.9 | 4.7 | 3.9 | 3.7 | 3.1 |
| 6.1 | 3.1 |
Resuma estos datos construyendo:
a. Una distribución de frecuencia porcentual. Utilice las clases 0.1 a 3; 3.1 a 6; etc.
b. Un histograma.
c. Una distribución de frecuencia porcentual acumulada.
d. Una ojiva.
e. ¿Qué porcentaje de personas utiliza la computadora 9 horas o menos?
f. ¿Son datos de series de tiempo o datos de sección transversal?
Ejercicio 2.
Cada año en Reino Unido, aproximadamente 1.5 millones de los estudiantes de educación superior presentan un examen de aptitud escolar. A continuación se presentan las puntuaciones obtenidas en las áreas de matemáticas y expresión verbal por una muestra de estudiantes durante la última aplicación de la prueba.
Tabla de Números
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1025 | 1042 | 1195 | 880 | 945 | 1102 | 845 | 1095 | 936 | 790 | 1097 | 913 | 1245 |
| 1040 | 998 | 998 | 940 | 1043 | 1048 | 1130 | 1017 | 1140 | 1030 | 1171 | 1035 |
a. Presente una distribución de frecuencia porcentual de estas puntuaciones. Utilice las clases 750-849, 850-949, etc.
b. Presente una distribución de frecuencia porcentual acumulada.
c. Elabore una ojiva.
d. ¿Qué porcentaje de estudiantes obtuvo una calificación menor a 950?
e. ¿Son datos de series de tiempo o datos de sección transversal?
Ejercicio 3.
La universidad cuenta con estadísticas sobre las áreas que son más elegidas por los estudiantes de nuevo ingreso. Las cinco más elegidas son arte y humanidades (A), administración de negocios (B), ingeniería (E), política (P), ciencias sociales (S) y otras áreas (O). Las siguientes fueron las áreas elegidas por 40 estudiantes de recién ingreso de una muestra.
Tabla de Letras Formando Palabras/Frases
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | P | O | O | E | E | B | B | A | S | O | A | E | B | E | O | E | Р | O | S | O | B | O | A | O |
| E | A | B | E | O | S | A | P | O | S | O | S | O | E | A | P | O | S | O | S | O | E |
a. Dé una distribución de frecuencia y otra de frecuencia porcentual.
b. Elabore una gráfica de barras.
c. ¿Cuál es el área más elegida por los estudiantes de nuevo ingreso? ¿Qué porcentaje de los estudiantes de nuevo ingreso elige esta área?
d. ¿Son datos de series de tiempo o datos de sección transversal?
e. ¿Cuál es la escala de medición adecuada para estos datos?